Un tipico problema di geometria ci chiede di trovare le dimensioni di un rettangolo di cui conosciamo l’area ed il rapporto tra base ed altezza. Vediamo come risolverlo.
Problema: Un rettangolo ha l’area di 225 cm2 e l’altezza è i quattro noni della base.
Per comprendere il procedimento è meglio disegnare la figura.

Se l’altezza è i 4/9 della base, questa sarà 9/9, quindi tutto il rettangolo è formato da 9×4=36 quadratini.
L’area di ciascun quadratino misura: area rettangolo diviso numero quadratini:
225 : 36 = 6,25 cm2
Adesso possiamo calcolare la lunghezza del lato di questo quadratino con la formula inversa che dice: lato quadrato = radice quadrata (area quadrato)
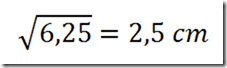
Infine calcoliamo la misura della base AB = 9 x 2,5 = 22,5 cm
e la misura dell’altezza BC = 4 x 2,5 = 10 cm

Grazie Stefania per il tuo commento!
Ogni passaggio spiegato in modo chiaro. Grazie
Di solito i problemi li risolviamo quando scrivete qui: vuoi un aiuto?
Come puoi dividere un rettangolo in triangoli equilateri?
Mandaci la figura!
Ciao!
Buongiorno abbiamo questo problema. Se conosco l’area di un rettangolo composto da 4 triangoli equilateri posso trovare l’area di uno di essi? Se sì perchè? E come si fa? Grazie per l’aiuto
Ciao Claudia. Se i dati cono corretti la radice di 77,(3) = 8,793… basta usare la calcolatrice 🙂
Ho un rettangolo con area 1160 cmq. Una dimensione è 3/5 dell’altra.
Faccio 3×5 =15
1160:15=77,3 periodico
Come faccio a fare la radice quadrata di un numero periodico?
Grazie
Ci dispiace… 🙁
Grazie comunque per aver visitato il nostro sito!
Saluti dall’Osmosi delle Idee
Non mi è stato utile
Ciao Martina, se conosci il perimetro allora conosci anche il semiperimetro (148 : 2 = 74) che è formato dalla somma delle due dimensioni (semiperimetro = base + altezza).
A questo punto il tuo problema diventa il classico: “conosco la somma e la differenza di due numeri, come trovo i due numeri?” la cui soluzione troverai leggendo qui, oppure qui.
Saluti.
il mio problema dice: calcola la lunghezza delle dimensioni di un rettangolo avente il perimetro di 148 cm sapendo che la loro differenza è 12 cm.
come faccio?
Bene! Ti siamo grati del commento 🙂
Mi è stato molto utile
Non si capisce nulla
Chiaro e utile! Il libro di mio figlio non spiegava come risolvere questo tipo di problema ma ora e’ tutto chiaro! Visiteremo ancora questo sito.
Molto bene! Siamo felicissimi di essere stati utili!
Grazie ragazzi, il compito di mia figlia per domani è risolto e, soprattutto, CAPITO!!!
Grazie,siete stati molto utili e visiteremo spesso il vostro sito.
Evviva! Siamo molto contenti di sapere che hai capito meglio questo genere di problemi! 🙂
Mi è stato utilissimo, sul mio libro di matematica ce ne sono a dozzine di questi problemi e ho iniziato a demoralizzarmi quando ho visto che erano in pratica uguali ma che io non ero in grado di risolverli…
Grazie mille quindi per avermeli fatti capire!
Un ringraziamento all’osmosi delle idee!!!!
Grazie di tutto!!!!!!!